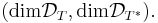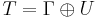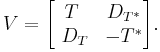Contraction (operator theory)

In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling. The analysis of contractions provides insight into the structure of operators, or a family of operators.

Contractions on a Hilbert space

Consider the special case where T is a contraction acting on a Hilbert space 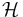$\mathcal{H}$ . We define some basic objects associated with T.

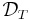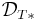The defect operators of T are the operators D_T = (1 − T*T)^½ and D_T* = (1 − TT*)^½. The square root is the positive semidefinite one given by the spectral theorem. The defect spaces $\mathcal{D}_T$ and $\mathcal{D}_{T*}$ are the ranges Ran(D_T) and Ran(D_T*) respectively.

The defect indices of T are the pair

$(\mbox{dim}\mathcal{D}_T, \mbox{dim}\mathcal{D}_{T^*}).$

The defect operators and the defect indices are a measure of the non-unitarity of T.

A contraction T on a Hilbert space can be canonically decomposed into an orthogonal direct sum

$T = \Gamma \oplus U$

where U is a unitary operator and Γ is completely non-unitary in the sense that it has no reducing subspaces on which its restriction is unitary. If U = 0, T is said to be a completely non-unitary contraction. A special case of this decomposition is the Wold decomposition for an isometry, where Γ is a proper isometry.

Sz.-Nagy's dilation theorem, proved in 1953, states that for any contraction T on a Hilbert space H, there is a unitary operator U on a larger Hilbert space K ⊇ H such that if P is the orthogonal projection of K onto H then Tⁿ =P Uⁿ P for all n > 0. The operator U is called a dilation of T and is uniquely determined if U is minimal, i.e. K is the smallest closed subspace invariant under U and U* containing H.

A direct construction of a unitary dilation of a contraction operator T' may be obtained as follows. Let V be the operator on

$H \oplus H$

defined by the matrix

$V = \begin{bmatrix} T & D_{T^*}\\ \ D_T & -T^* \end{bmatrix}.$

V is clearly a dilation of T. It may be shown that V is unitary, therefore an unitary dilation of T, sometimes called the Julia operator of T.

Contractions on Hilbert spaces can be viewed as the operator analogs of cos θ and are called operator angles in some contexts. The explicit description of contractions leads to (operator-)parametrizations of positive and unitary matrices.

References

Sz.-Nagy, B.; Foias, C.; Bercovici, H.; Kérchy, L. (2010), Harmonic analysis of operators on Hilbert space, Universitext (Second ed.), Springer, ISBN 978-1-4419-6093-1
Riesz, F.; Sz.-Nagy, B. (1995), Functional analysis. Reprint of the 1955 original, Dover Books on Advanced Mathematics, Dover, pp. 466-472, ISBN 0-486-66289-6

Contraction (operator theory)

Contractions on a Hilbert space

See also

References